协同过滤（Collaborative Filtering, CF）是推荐算法的一种，他根据许多用户的偏好信息(这是协同部分)推荐商品(这是过滤部分)。这种方法利用用户偏好行为的相似性，给定用户和物品之间的先前交互，推荐算法学习预测未来的交互。这些推荐系统根据用户过去的行为建立一个模型，比如以前购买的商品或对这些商品的评级以及类似的决策。

协同过滤算法按照目标可分为两类：

基于用户的协同过滤
考虑用户兴趣的一种方法是寻找与他在某种程度上相似的用户，然后建议这些用户感兴趣的东西。
基于项的协同过滤
另一种方法是直接计算兴趣之间的相似度。然后，我们可以通过汇总与每个用户当前兴趣相似的兴趣，为每个用户生成建议。

而其中，相似度计算是推荐系统中协同过滤算法的核心。

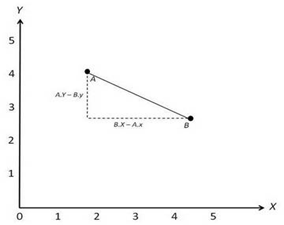
欧式距离

类比几何中两个点的距离，其计算方式也跟几何中的一模一样

欧氏距离

实现代码：

import numpy as np


vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

d = np.linalg.norm(vec1-vec2, ord=2)
# 或者
d = np.sqrt(np.sum(np.square(vec1-vec2)))

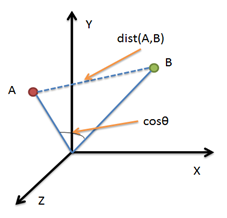
余弦相似度

通过计算两个向量之间的夹角余弦值来衡量它们的相似性。如果余弦值接近1，则说明两个向量方向相似，表示用户或物品的偏好接近；如果接近0，则说明相似性低。其计算方法即为计算两个向量夹角度数

\text{Cosine Similarity} = \frac{\vec{A} \cdot \vec{B}}{||\vec{A}|| \times ||\vec{B}||} = \frac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \times \sqrt{\sum_{i=1}^{n} B_i^2}}

实现代码

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

d = np.dot(vec1,vec2)/(np.linalg.norm(vec1)*(np.linalg.norm(vec2)))

皮尔逊相关系数

其实质是协方差与标准差的比值，衡量两个变量之间的线性相关性，取值范围在-1到1之间。系数为1表示完全正相关，-1表示完全负相关，0表示没有相关性。原理跟余弦相似度有点像，p的一个几何解释是其代表两个变量的取值根据均值集中后构成的向量之间夹角的余弦.

\text{P}(A, B) = \frac{\sum_{i=1}^{n} (A_i - \bar{A})(B_i - \bar{B})}{\sqrt{\sum_{i=1}^{n} (A_i - \bar{A})^2} \times \sqrt{\sum_{i=1}^{n} (B_i - \bar{B})^2}}

范围：[-1,1]，绝对值越大，说明相关性越强，负相关对于推荐的意义小。

该相似度并不是最好的选择，也不是最坏的选择，只是因为其容易理解，在早期研究中经常被提起。使用Pearson线性相关系数必须假设数据是成对地从正态分布中取得的，并且数据至少在逻辑范畴内必须是等间距的数据。Mahout中，为皮尔森相关计算提供了一个扩展，通过增加一个枚举类型（Weighting）的参数来使得重叠数也成为计算相似度的影响因子。

实现代码：

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

p = np.corrcoef(vec1, vec2)

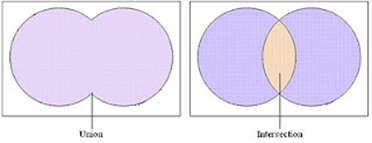
杰卡德相似系数

通过计算两个集合的交集与并集的比值。其值介于0和1之间，1表示完全相同，0表示完全不同。比较两个集合是否相似，就是比较这两个集合共有元素的占比。因为集合具有互异性，集合中任意两个元素都是不同的对象，集合A中的任意一个元素在集合B中只有两种状态，即有或者没有，但无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。因此，杰卡德系数可以用来计算非对称二元属性对象的相似性。

\text{Jaccard}(A, B) = \frac{|A \cap B|}{|A \cup B|}

杰卡德

实现代码：

import numpy as np
import scipy.spatial.distance as dist

vec1 = np.array([1, 1, 0, 1, 0, 1, 0, 0, 1])
vec2 = np.array([0, 1, 1, 0, 0, 0, 1, 1, 1])

d = dist.pdist(np.array([vec1, vec2]), "jaccard")

曼哈顿距离

是欧式距离的一种变体，通常用于网格状空间中，相较于欧式距离，曼哈顿距离不会受到数据点分布的影响，其计算公式为：

d(x, y) = |x_1 - y_1| + |x_2 - y_2| + \dots + |x_n - y_n|

其中， $x = (x_1, x_2, \dots, x_n)$ 和 $y = (y_1, y_2, \dots, y_n)$ 是两个点的坐标。

实现代码：

def manhattan_distance_np(x, y):
    return np.sum(np.abs(np.array(x) - np.array(y)))

切比雪夫距离(Chebyshev Distance)

切比雪夫距离是计算每个维度差的绝对值，并选取其中的最大值。它表示两个点之间的“最短”路径，在所有维度中，最大的差值决定了最终的距离,其计算公式如下：

d_{\text{Chebyshev}}(x, y) = \max \left( |x_1 - y_1|, |x_2 - y_2|, \dots, |x_n - y_n| \right)

实现代码：

def chebyshev_distance(x, y):
    if len(x) != len(y):
        raise ValueError("输入向量的维度必须相同")
    
    distance = max(abs(x_i - y_i) for x_i, y_i in zip(x, y))
    
    return distance

协同过滤中的相似度计算方法

欧式距离

余弦相似度

皮尔逊相关系数

杰卡德相似系数

曼哈顿距离

切比雪夫距离(Chebyshev Distance)